Zenone di Elea è un logico e filosofo greco che è principalmente noto per i paradossi nominati in suo onore. Non si sa molto della sua vita. La città natale di Zenone è Elea. Anche negli scritti di Platone fu menzionato l'incontro del filosofo con Socrate.
Intorno al 465 a.C. e. Zenone ha scritto un libro in cui ha delineato tutte le sue idee. Ma, sfortunatamente, non ha raggiunto i nostri giorni. Secondo la leggenda, il filosofo morì in una battaglia con un tiranno (presumibilmente il capo di Elea Nearch). Tutte le informazioni su Elea furono raccolte a poco a poco: dalle opere di Platone (nato 60 anni dopo Zenone), Aristotele e Diogene Laertius, che tre secoli dopo scrisse un libro di biografie di filosofi greci. Zenone è anche menzionato negli scritti dei successivi rappresentanti della scuola di filosofia greca: Temistia (IV secolo d.C.), Alexander Afrodinsky (III secolo d.C.), Filoponte e Simplicius (entrambi vissuti nel VI secolo d.C.). Inoltre, i dati di queste fonti sono così ben coerenti tra loro che tutte le idee del filosofo possono essere ricostruite da esse. In questo articolo ti parleremo dei paradossi di Zenone. Quindi cominciamo.

Paradossi del set
Sin dall'era di Pitagora, lo spazio e il tempo erano considerati esclusivamente dal punto di vista della matematica. Cioè, si credeva che fossero composti da molti punti e punti. Tuttavia, hanno una proprietà che è più facile da percepire che da definire, vale a dire la "continuità". Alcuni paradossi di Zenone dimostrano che non può essere diviso in momenti o punti. Il ragionamento del filosofo si riduce a quanto segue: “Supponiamo di aver completato la divisione fino alla fine. Quindi solo una delle due opzioni è vera: o otteniamo le quantità minime possibili o le parti che sono indivisibili, ma infinite in quantità, o la divisione ci porterà a parti senza grandezza, poiché la continuità, essendo omogenea, deve essere divisibile in qualsiasi circostanza. Non può essere divisibile in una parte, ma non nell'altra. Sfortunatamente, entrambi i risultati sono piuttosto ridicoli. Il primo è dovuto al fatto che il processo di divisione non può terminare mentre ci sono parti nel resto che hanno un valore. E il secondo è perché in una situazione del genere, inizialmente il tutto sarebbe stato formato dal nulla ”. Simplicio attribuì questo argomento a Parmenide, ma è più probabile che il suo autore sia Zenone. Andiamo oltre.
I paradossi del movimento di Zenone
Sono considerati nella maggior parte dei libri dedicati al filosofo, perché entrano in dissonanza con l'evidenza dei sentimenti degli eleatici. In relazione al movimento, si distinguono i seguenti paradossi Zenoni: "Freccia", "Dichotomia", "Achille" e "Fasi". E sono venuti da noi grazie ad Aristotele. Diamo un'occhiata più da vicino a loro.
"Arrow"
Un altro nome è il paradosso quantistico di Zenone. Il filosofo afferma che qualsiasi cosa o si ferma o si muove. Ma nulla è in movimento se lo spazio occupato è uguale ad esso in lunghezza. Ad un certo momento, la freccia in movimento si trova in un punto. Pertanto, non si muove. Simplicio formulò questo paradosso in forma abbreviata: “Un oggetto volante occupa un posto uguale nello spazio, ma ciò che occupa un posto uguale nello spazio non si muove. Pertanto, la freccia è ferma. " Femistius e Phelopon hanno formulato opzioni simili.
"Dicotomia"
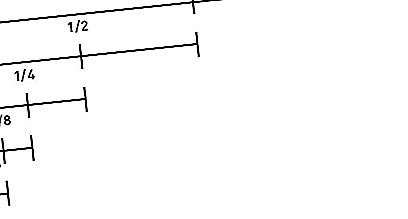
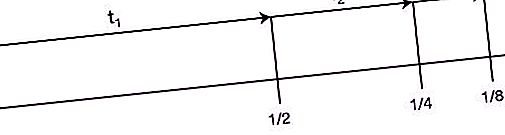
Prende il secondo posto nella lista dei "Paradossi di Zeno". Si legge come segue: “Prima che un oggetto che inizia a muoversi possa percorrere una certa distanza, deve superare metà di questo percorso, quindi metà del rimanente, ecc. All'infinito. Poiché durante ripetute divisioni della distanza a metà, il segmento diventa sempre finito e il numero di questi segmenti è infinito, questa distanza non può essere superata in un tempo finito. Inoltre, questo argomento è vero sia per le piccole distanze che per le alte velocità. Pertanto, qualsiasi movimento è impossibile. Cioè, il corridore non sarà nemmeno in grado di iniziare."
Questo paradosso ha commentato dettagliatamente Simplicius, indicando che in questo caso un numero infinito di tocchi deve essere fatto in un tempo finito. "Chiunque tocchi qualcosa può contare, ma l'insieme infinito non può essere risolto o contato." Oppure, come ha detto Philopon, un insieme infinito è indefinibile.
"Achille"
Conosciuto anche come il paradosso della tartaruga zeno. Questa è l'argomento filosofico più popolare. In questo paradosso del movimento, Achille compete in una corsa con una tartaruga, che all'inizio ha un piccolo handicap. Il paradosso è che la guerriera greca non sarà in grado di raggiungere la tartaruga, dal momento che prima raggiungerà il punto di partenza e lei sarà già al punto successivo. Cioè, la tartaruga sarà sempre davanti ad Achille.
Questo paradosso è molto simile a una dicotomia, ma qui la divisione infinita va secondo la progressione. Nel caso di una dicotomia, c'è stata una regressione. Ad esempio, lo stesso corridore non può iniziare, perché non può lasciare la sua posizione. E nella situazione con Achille, anche se il corridore inizia a muoversi, continuerà a non correre da nessuna parte.
"Flock"
Se confrontiamo tutti i paradossi di Zenone in termini di complessità, allora questo sarebbe il vincitore. È più difficile da spiegare di altri. Simplicio e Aristotele descrissero questo ragionamento in modo frammentario e non si può fare affidamento sulla sua affidabilità con certezza al 100%. La ricostruzione di questo paradosso ha la seguente forma: che A1, A2, A3 e A4 siano corpi immobili di uguali dimensioni, e B1, B2, B3 e B4 siano corpi delle stesse dimensioni di corpi A. B si spostano a destra in modo che ogni B passi E in un istante, che è il più piccolo periodo di tempo possibile. Lascia che B1, B2, B3 e B4 siano corpi identici a A e B e muoviti rispetto ad A a sinistra, superando ciascuno dei corpi in un istante.
Ovviamente, B1 ha superato tutti e quattro i corpi di B. Prendiamo per un'unità il tempo impiegato da un corpo di B per attraversare un corpo di B. In questo caso, per ogni movimento erano necessarie quattro unità. Tuttavia, si riteneva che i due momenti trascorsi per questo movimento fossero minimi e quindi indivisibili. Ne consegue che quattro unità indivisibili sono uguali a due unità indivisibili.